by Emily Pentil, Year 11, Sir Henry Floyd Grammar School, Buckinghamshire.
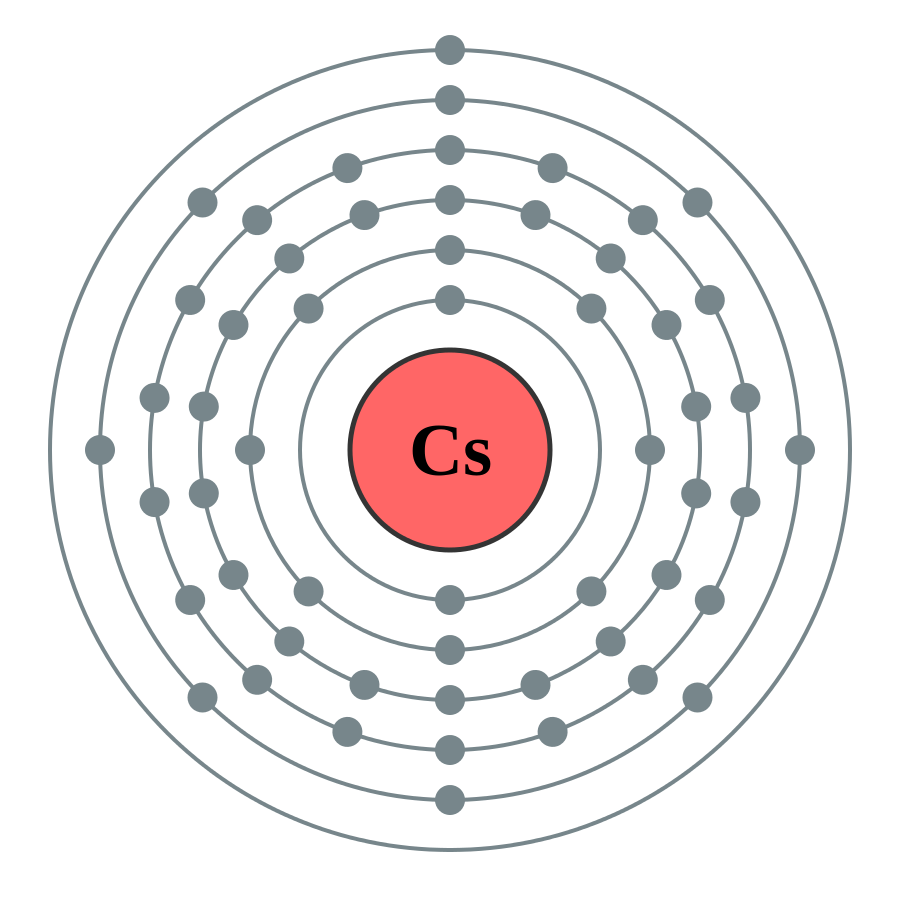
In 1957, one second was defined as 9,192,631,770 oscillations of the radiation corresponding to the transition between two energy levels of the caesium atom. Physics so esoteric seems unlikely to feature in an essay about the science of everyday life. But the idea of atomic time makes possible the Global Positioning System; one of the greatest inventions of the 21st century (ask anyone desperately lost).
The GPS network consists of 24 satellites, 4 will have a line of visibility to your receiver at all times. Your device receives a radio signal from several satellites. The satellites transmit the time the signals are sent, and by comparing the time the signal left the satellite with the time it was received, the time taken for the signal to reach the receiver can be found. Combining this value with the known speed of electromagnetic radiation allows the distance to be calculated. With one satellite this is useless; all the receiver knows is that it’s a certain radius away from the satellite. But with 4 satellites, the possible location of the receiver is limited to the point where it can determine position in three dimensions. The satellite (which synchronises with the receiver) needs to know the time precisely: an error of a single microsecond translates into a discrepancy of 300m.
The trick to keeping time is counting the interval between something steadily repeating; a swinging pendulum or some number of ‘Mississippis’. One second could be defined as the period of a certain pendulum, the time it takes for it to swing in one direction and back. This idea can also be expressed by saying the frequency, the number of full swings per second, is 1. Quartz vibrates at 32768 Hz, pulses per second, when a current is applied. For our purpose, however, even the best mechanical pendulums and quartz crystals won’t cut it. Atomic clocks can reach extraordinary degrees of accuracy, with the NIST-F1 losing only 1 second in over 100 million years. How?
Firstly, we’ve got to delve into the atomic realm. A caesium atom has one electron in its outer shell, and how this electron interacts with the atomic nucleus is the first piece of the puzzle. The ‘spin’ and orbit of the electron coupled with the spin of the nucleus about its own axis gives rise to a hyperfine structure. ‘Hyperfine’ because slight, specific energy changes do not cause the electron to jump from one energy level to another, but to oscillate between sub-levels. Microwaves with very specific energies are needed for a hyperfine level transition to occur (energy and therefore energy level transitions are quantised, meaning they can only have certain values). The energy of an electromagnetic wave is determined by its frequency. The period, time taken for a single oscillation, of our atomic pendulum is 1/9,192,631,770 of a second.
Resonance occurs when an already oscillating system is made to oscillate by an outside source at a frequency equal to to its own natural frequency, resulting in a larger amplitude. You’ve encountered resonance before if you’ve ever pushed someone on a swing – going against the swings ‘natural frequency’ is equivalent to pushing forward while the swing is still moving downwards (and risking your teeth in the process). When you push at the right time you can increase the maximum height the swing will get to with very little force.
In an atomic clock, caesium atoms flowing through a tube are bombarded with microwaves. If the microwaves are the resonant frequency (energy), the caesium atoms resonate, oscillating between two states with a larger amplitude. A detector at the end of the tube tracks how many atoms have reached a higher energy state. The more finely tuned the microwave frequency is to 9,192,631,770 cycles per second, the more high energy caesium atoms reach the detector. If the peak number of these caesium atoms reach the detector, then we know the microwaves have a constant frequency. If not all the caesium has been energised, this means the frequency has changed slightly. A signal is sent back to the microwave generator telling it to change its frequency. This feedback loop is what makes atomic clocks so accurate, and an everyday marvel of physics.